Answer:
Segments DE and BC have equal slopes, showing that segments DE and BC are parallel
Explanation:
Here we have the coordinates as follows
The coordinates of A is (4, 6)
The coordinates of B is (2, -2)
The coordinates of C is (-2, -4)
Therefore, the coordinates of D the midpoint AB is ((4 + 2)/2, (6 - 2)/2) which gives;
The coordinates of D is (3, 2)
Similarly, the coordinates of E the midpoint AC is ((4 - 2)/2, (6 - 4)/2) which gives;
The coordinates of E is (1, 1)
To prove that segment DE is parallel to segment BC, e show that the slopes of the two segments are equal as follows;
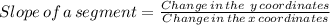
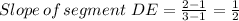
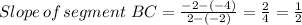
Therefore, the slopes of segments DE and BC are equal, which shows that segment DE is parallel to BC.