Answer:
a)
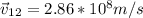
b)
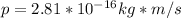
Step-by-step explanation:
a) When we have two particles traveling in parallel directions, the formula for relative velocity is:
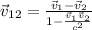
Here we have that v(1) = -v(2), the speed of the of the second particle is the negative of the first one.
If we use these equivalence we have:
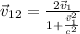
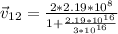
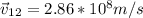
And,
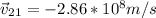
b) The relativistic momentum equation to one particle observed by the other particle, is:
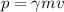
Where gamma is:
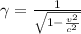
- v is the speed of the first particle relative to the second particle (
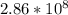 )
) - m is the mass of the particle
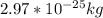
Then gamma will be:
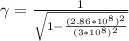
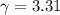
Finally, the value of the momentum will be:
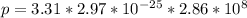
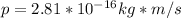
I hope it helps you!