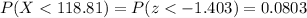Question

The quality control manager at a computer manufacturing company believes that the mean life of a computer is 120 months, with a variance of 64. If he is correct, what is the probability that the mean of a sample of 89 computers would be less than 118.81 months? Round your answer to four decimal places.

Answer 1

P(X<118.81)=0.0803

Explanation:

Assuming the distribution for the mean life is approximately normal, with mean 120 months and variance 64 months^2, we can calculate the parameters for a sampling distribution with sample size = 89 computers.

The sampling distribution mean will be equal to the mean for a single computer:

`\mu_(89)=\mu=120`

The standard deviation will be adjusted by the sample size as:

`\sigma_(89)=√(\sigma^2/n)=√(64/89)=√(0.719)=0.848`

With these parameters, we can calculate the z-score for X=118.81.

`z=(X-\mu)/(\sigma)=(118.81-120)/(0.848)=(-1.19)/(0.848)=-1.403`

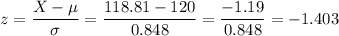
Then, the probability that the mean of a sample of 89 computers is less than 118.81 months is:

`P(X<118.81)=P(z<-1.403)=0.0803`