Question

Rewrite the equation by completing the square. X2−2x+1=0x^{2}-2x+1 = 0x2−2x+1=0x, squared, minus, 2, x, plus, 1, equals, 0 (x+(x + {}(x+left parenthesis, x, plus )2=)^2 = {})2=right parenthesis, squared, equals

Answer 1

Rewriting
`2x^2-2x+1=0` equation we get
`(x-1) ^2`=0.

Given the quadratic equation

`2x^2-2x+1=0`

the process of completing the square involves manipulating the equation to a form that expresses a perfect square trinomial.

First, move the constant term to the right-hand side, resulting in

`x^2` −2x−1=0.

Next, halve the coefficient of x, yielding

−2/2=−1

Squaring this result
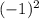`(-1)^2` gives 1.

Add this value to both sides of the equation:

=
`x^2` −2x +
`(-1) ^2`

= −1 +
`(-1) ^2`

leading to

`(x-1) ^2`=0

Upon simplification,

x−1 squared equals zero.

Therefore, the equation rewritten by completing the square is

`(x-1) ^2`=0, indicating that the solution involves a perfect square binomial with a value of zero.