Question

Leanne is trying to convert x^2+4x-6=0 the standard form to vertex form by completing the square which equation shows the correct form

Answer 1

Answer:
`(x+2)^2-10=0`

Explanation:

`x^2+4x-6=0`

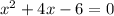
Let 0 = y to not mix up the numbers.

`x^2+4x-6=y`

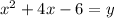
we are trying to get to this form:
`y=a(x-h)^2+k`

Let's group the variables to make it easier for us to complete the square.

`(x^2+4x)-6=y`

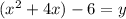
Complete the square by taking the number next to the x variable (4) divide it by 2 (4/2=2) and square it (
`2^2=4`)

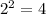Add this.

`(x^2+4x+4)-6=y`

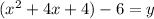
You also have to add it to the right side, but since we're looking to isolate y again, we're going to have to move it to the left side eventually; therefore, we can simply change the sign and add it to the left side.

In other words, instead of doing this:

`-6=y+4\\-6-4=y`

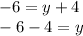
I'm going to directly say the opposite of +4 is -4

`(x^2+4x+4)-6-4=y`

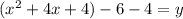
Now factor the parentheses and combine like terms;

`(x+2)^2-10=y`

And like we said y = 0, so change that...

`(x+2)^2-10=0`

Answer 2

In vertex form we have y = (x + 2)^2 - 10

Explanation:

x^2+4x-6=0 is in standard form; we want it in the form y - k = a(x - h)^2.

Complete the square within x^2+4x-6=0

We get x^2 + 4x - 6 = 0 => x^2 + 4x + 4 - 4 - 6, or

y = (x + 2)^2 - 10

Comparing this to y = (x - h)^2 - 10, we see that the vertex is at

(h, k) : (-2, -10)