Question

The sides of two similar hexagons are in a ratio of 3:7. The area of the smaller hexagon is 36in2. Find the area of the larger hexagon.

Answer 1

The area of the larger hexagon is 196 in²

Explanation:

Area of a regular hexagon is given as;

`A = ((3√(3) )/(2) )a^2`

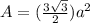
where;

a is side of the hexagon

Given the area of the smaller hexagon as 36in², we now determine the side of this smaller hexagon.

`A = ((3√(3) )/(2) )a^2`

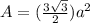
A = (2.59808)a²

a² = A / (2.59808)

a² = 36in² / (2.59808)

a² = 13.8564 in²

a = √ 13.8564 in²

a = 3.7224 in

let the side of the larger hexagon = b

Given the ratio of the sides of small to large hexagon as 3:7,

a:b = 3:7

`(a)/(b) = (3)/(7) \\\\(3.7224)/(b) = (3)/(7) \\\\b = (3.7224*7)/(3) = 8.6856 \ in`

Now, with the side of the larger hexagon known, we calculate its area.

A = (2.59808)b²

A = (2.59808)(8.6856)²

A = 196 in²

Therefore, the area of the larger hexagon is 196 in²