Question

PLEASE HELP ASAP!!!!!!!!

The function below represents the height, in feet, of the rocket, and t represents the time, in seconds, since the rocket was launched.

h(t) = -16t^2 + 72t + 7

State how long it takes the rocket to hit the ground to the nearest tenth of a second as only a number without units.

Answer 1

4.6.

Explanation:

The rocket hits the ground when h(t) = 0. So

`-16t^(2) + 72t + 7 = 0`

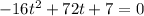
Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

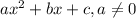This polynomial has roots
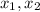`x_(1), x_(2)` such that
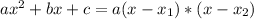`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

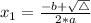
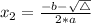
In this question:

`-16t^(2) + 72t + 7 = 0`

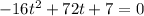
So

`a = -16, b = 72, c = 7`

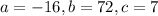
Then

`\bigtriangleup = 72^(2) - 4*(-16)*7 = 5632`

`t_(1) = (-72 + √(5632))/(2*(-16)) = -0.1`

`t_(2) = (-72 - √(5632))/(2*(-16)) = 4.6`

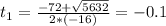
Time is a positive measure, so the answer is 4.6.