Answer:
The sharing cone holds about 9 times more popcorn than the skinny cone.
Explanation:
The volume of a cone is given by the following formula:
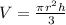
In which r is the radius and h is the height.
Two cones:
Both have the same height.
The sharing-size cone has 3 times the radius of the skinny-size cone.
Skinny:
radius r, height h. So
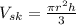
Sharing size:
radius 3r, height h. So
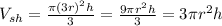
About how many times more popcorn does the sharing cone hold than the skinny cone?
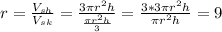
The sharing cone holds about 9 times more popcorn than the skinny cone.