Answer: Mean of the sample proportion = 74.4
Standard deviation of the samnple proportion is 5.32.
Explanation:
Given : A random sample of 120 is taken from a population of 10000.
Let n = 120
Also, from previous survey, it is believed that 62% of the population has an Instagram account.
i.e, population proportion : p = 0.62
Now , the mean of the sample proportin would be :
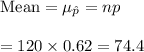
i.e. Mean of the sample proportion = 74.4
The standard deviation of the samnple proportion would be :

Thus , the standard deviation of the samnple proportion is 5.32.