Question

10.

83 random samples were selected from a normally distributed population and were found to have a mean of 32.1 and a standard deviation of 2.4. Construct a 90% confidence interval for the population standard deviation.

A.
2.2 < σ < 2.8

B.
28.8 < σ < 37.4

C.
4.6 < σ < 7.8

D.
1.4 < σ < 1.8

Answer 1

`((82)(2.4)^2)/(104.139) \leq \sigma^2 \leq ((82)(2.4)^2)/(62.132)`

`4.535 \leq \sigma^2 \leq 7.602`

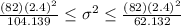
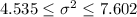
Now we just take square root on both sides of the interval and we got:

`2.2 \leq \sigma \leq 2.8`

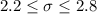
And the best option would be:

A. 2.2 < σ < 2.8

Explanation:

Information provided

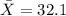`\bar X=32.1` represent the sample mean

`\mu` population mean

s=2.4 represent the sample standard deviation

n=83 represent the sample size

Confidence interval

The confidence interval for the population variance is given by the following formula:

`((n-1)s^2)/(\chi^2_(\alpha/2)) \leq \sigma^2 \leq ((n-1)s^2)/(\chi^2_(1-\alpha/2))`

The degrees of freedom are given by:

`df=n-1=83-1=82`

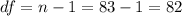
The Confidence is given by 0.90 or 90%, the value of
`\alpha=0.1` and
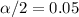`\alpha/2 =0.05`, the critical values for this case are:

`\chi^2_(\alpha/2)=62.132`

`\chi^2_(1- \alpha/2)=104.139`

And replacing into the formula for the interval we got:

`((82)(2.4)^2)/(104.139) \leq \sigma^2 \leq ((82)(2.4)^2)/(62.132)`

`4.535 \leq \sigma^2 \leq 7.602`

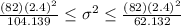
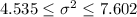
Now we just take square root on both sides of the interval and we got:

`2.2 \leq \sigma \leq 2.8`

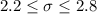
And the best option would be:

A. 2.2 < σ < 2.8