Answer:
(a) Probability that the number who have graduated from college is exactly 175 is 0.0398.
(b) Probability that the number who have graduated from college is less than 200 is 0.9889.
Explanation:
We are given that about 35% of U.S. workers are college graduates. You randomly select 500 U.S. workers and ask them whether they are college graduates.
The above situation can be represented through binomial distribution but we will approximate it to normal distribution because the sample size is very large.
So, the z score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where, X = Number of workers who have graduated from college
 = population mean =
= population mean =
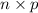
=
 = 175
= 175
 = standard deviation =
= standard deviation =
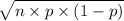
=
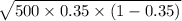 = 10.66
= 10.66
Note : We will also use the concept of continuity correction here.
(a) Probability that the number who have graduated from college is exactly 175 is given by = P(174.5 < X < 175.5)
P(174.5 < X < 175.5) = P(
 < Z <
< Z <
 ) = P(
) = P(
 < Z <
< Z <
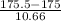 )
)
= P(-0.05 < Z < 0.05) = P(Z < 0.05) - P(Z < -0.05)
= P(Z < 0.05) - [1 - P(Z < 0.05)]
= 0.51994 - 0.4801 = 0.0398
(b) Probability that the number who have graduated from college is less than 200 is given by = P(X < 200) = P(X
 199.5)
199.5)
P(X
 199.5) = P(
199.5) = P(


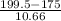 ) = P(Z
) = P(Z
 2.29) = 0.9889
2.29) = 0.9889