Start with your explicit formula which I have provided for you below.

In the formula, the n represents what term we want to find.
Since we want to find the 52nd term, we plug 52 in for n.
Then,
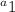 represents our first term in the sequence which is -3.
represents our first term in the sequence which is -3.
Now, d is the difference between each of the terms and it's 15.
So we have
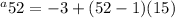 .
.
Now just simplify from here.
First, apply order of operations (inside parentheses first).
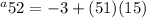 .
.
Now, multiply before we add.
 .
.
Now just add to get
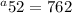 .
.