Question

A basketball player is 7 ft tall. He shoots the ball into the basket and the path of the

ball makes a quadratic equation. This could be shown with the equation h(t) == 15t^2+ 30t+7

where t is the time in seconds after the ball was shot and h is the height. What will the

ball's maximum height be?

Answer 1

52

Explanation:

Given the the equation h(t) =-
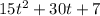`15t^2+ 30t+7` where t is the time in second

So to find the ball's maximum height we can apply the vertex formula:

t=
`(-b)/(2a)`

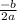
to find the "x" value of the vertex, then plug that value into the original equation as a substitute for "x".

Standard quadratic form is:
`ax^2+bx+c`

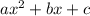
=> a=15, b=30 in our given equation

<=> t =
`(-30)/(2*-15) =1`

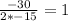
When t =-1 we have h(t) =
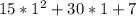`15*1^2+ 30*1+7` = 52

So the ball's maximum height is: 52

Hope it will find you well.