Question

A ball is thrown downward from the top of a 120-foot building with an initial velocity of 14 feet per second. The hoight of the ball h after t

seconds is given by the equation h= - 16 - 14 +120


How long after the ball is thrown will it strike the ground?

Answer 1

Correct question:

A ball is thrown downward from the top of a 120-foot building with an initial velocity of 14 feet per second. The hoight of the ball h after t seconds is given by the equation

h= -16t² -14t +120

How long after the ball is thrown will it strike the ground?

Answer:

2.34 seconds

Explanation:

Given:

Height of building = 120 ft

Initial velocity, u = 14 ft/sec

h = -16t² -14t +120

h(t) = -16t² -14t +120

Let's find t when h(t) = 0

Let's factorize the equation,

-2(8t² + 7t - 60) = 0

We now have a quadartic equation:

8t² + 7 - 60 = 0

This equation cannot be factorized easily, so let's take the quadartic formula:

`t = ([-b +/- √((b^2-4ac))])/(2a)`

where a=8, b=7, c=-60

Substituting figures, we have:

`t = ([-7 +/- √((7^2 - 4(8)(-60)))])/(2*8)`

`t = ([-7 +/- √((49 - (-1920)))])/(16)`

`t = ([-7 +/- 44.37])/(16)`

Since we can't have a negitive sign, let's take the "+" sign

`t = ((-7 + 44.37))/(16)`

`t = (37.37)/(16)`

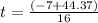
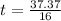
t = 2.34

The ball will hit the ground at 2.34 seconds