Question

A box with no top is to be constructed from a piece of cardboard whose length measures 10 inches more than its width. The box is formed by cutting squares that measure 4 inches on each side from the four corners and then folding up the sides. If the volume of the box will be 300 cubic inches what are the dimensions of the piece of cardboard?

Answer 1

• Width=10 Inches
• Length =20 Inches

Explanation:

Let the width of the cardboard=w in.

Since the length measures 10 inches more than its width, Length, l=(w+10) in.

The box is formed by cutting squares that measure 4 inches on each side from the four corners.

Therefore, we subtract 4 inches from each side of the dimension.

Width of the box=(w-8) in.

Length of the box=w+10-8=(w+2) in.

The part that will be folded up is the rectangle left in the sides after cutting out the squares, therefore:

Height of the box=4 Inches

Now, Volume of the box = 300 cubic inches

Therefore:

4(w-8)(w+2)=300

Divide both sides by 4

`(w-8)(w+2)=75\\$Expand\\w^2+2w-8w-16-75=0\\w^2-6w-91=0\\w^2-13w+7w-91=0\\w(w-13)+7(w-13)=0\\(w-13)(w+7)=0\\w-13=0$ or w+7=0\\w=13 inches`

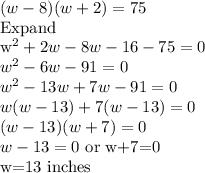
Therefore, the dimensions of the piece of cardboard are:

Width=10 Inches

Length =10+10 =20 Inches