Question

A company determines that its marginal revenue per day is given by R'(t), where R(t) is the total accumulated revenue, in dollars, on the tth day. The company's marginal cost per day is given by C'(t), where C(t) is the total accumulated cost, in dollars, on the tth day.

R'(t)=120e^t R(0)=0 C'(t)=120-0.6t C(0)=0

a. Find the total profit P(T) from t=0 to t=10

b. Find the average daily profit for the first ten days.

Answer 1

a) $2,641,885.90

b) $264,188.59

Explanation:

The total profit is the integral of the marginal profit. The marginal profit is the difference between marginal revenue and marginal cost.

`\displaystyle P(t)=\int^t_0 {(R'(t)-C'(t))} \, dt=\int^t_0{(120e^t-120+0.6t)}\,dt\\\\P(t)=120(e^t-1)-120t+0.3t^2`

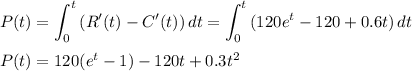
a) To find the total profit for the first 10 days, we evaluate P(10):

P(10) = 120(e^10 -1) -120(10) +0.3(10^2) = 120(22026.4658 -1) -1200 +30

P(10) = 2,641,885.90 . . . . rounded to cents

The total profit from day 0 to day 10 is $2,641,885.90.

__

b) The average daily profit is the total profit divided by the number of days:

average profit per day = P(10)/10 = $264,188.59

The average daily profit for the first 10 days is $264,188.59.