Answer:
A_max = 11250 ft^2
Explanation:
You have the following function for the area of the backyard:
 (1)
(1)
To find the maximum area, you first derivative the function A respect to x:
![(dA)/(dx)=(d)/(dx)[300x-2x^2]=300-4x](https://img.qammunity.org/2021/formulas/mathematics/college/kanjmueqnv7n85ktu0vy4qj6kroave3mib.png) (2)
(2)
Next, you equal the function (2) to zero in order to obtain the value of x:
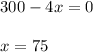
Finally, you replace the value of x=75 in the function A in (1):
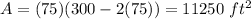
hence, the maximum area is 11250 ft^2