Question

A line tangent to the curve f(x)=1/(2^2x) at the point (a, f(a)) has a slope of -1. What is the x-intercept of this tangent?

Answer 1

x-intercept = 0.956

Explanation:

You have the function f(x) given by:

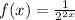`f(x)=(1)/(2^(2x))` (1)

Furthermore you have that at the point (a,f(a)) the tangent line to that point has a slope of -1.

You first derivative the function f(x):

`(df)/(dx)=(d)/(dx)[(1)/(2^(2x))]` (2)

To solve this derivative you use the following derivative formula:

`(d)/(dx)b^u=b^ulnb(du)/(dx)`

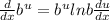
For the derivative in (2) you have that b=2 and u=2x. You use the last expression in (2) and you obtain:

`(d)/(dx)[2^(-2x)]=2^(-2x)(ln2)(-2)`

You equal the last result to the value of the slope of the tangent line, because the derivative of a function is also its slope.

`-2(ln2)2^(-2x)=-1`

Next, from the last equation you can calculate the value of "a", by doing x=a. Furhtermore, by applying properties of logarithms you obtain:

`-2(ln2)2^(-2a)=-1 \\\\2^(2a)=2(ln2)=1.386\\\\log_22^(2a)=log_2(1.386)\\\\2a=(log(1.386))/(log(2))\\\\a=0.235`

With this value you calculate f(a):

`f(a)=(1)/(2^(2(0.235)))=0.721`

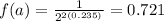
Next, you use the general equation of line:

`y-y_o=m(x-x_o)`

for xo = a = 0.235 and yo = f(a) = 0.721:

`y-0.721=(-1)(x-0.235)\\\\y=-x+0.956`

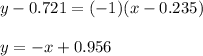
The last is the equation of the tangent line at the point (a,f(a)).

Finally, to find the x-intercept you equal the function y to zero and calculate x:

`0=-x+0.956\\\\x=0.956`

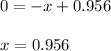
hence, the x-intercept of the tangent line is 0.956