Answer:
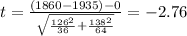
Now we can calculate the p value:
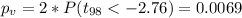
For this case the p value is a very lowe value so then we have enough evidence to reject the null hypothesis. Since the p value is a very low value.
Explanation:
Information given
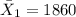 represent the mean for Grand Bahamas
represent the mean for Grand Bahamas
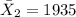 represent the mean for New Province
represent the mean for New Province
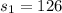 represent the sample standard deviation for Grand Bahamas
represent the sample standard deviation for Grand Bahamas
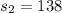 represent the sample standard deviation for New Bahamas
represent the sample standard deviation for New Bahamas
 sample size for the group Grand Bahamas
sample size for the group Grand Bahamas
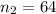 sample size for the group New Bahamas
sample size for the group New Bahamas
t would represent the statistic
System of hypothesis
We need to conduct a hypothesis in order to check if the difference in the population means, the system of hypothesis would be:
Null hypothesis:
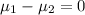
Alternative hypothesis:
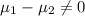
The statistic is given by:
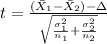 (1)
(1)
And the degrees of freedom are given by
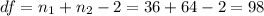
The statistic can be calculated like this:
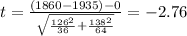
Now we can calculate the p value:
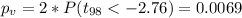
For this case the p value is a very lowe value so then we have enough evidence to reject the null hypothesis. Since the p value is a very low value.