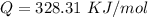Answer:
The activation energy is
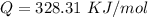
Step-by-step explanation:
From the question we are told that
The rate constant is k
at the temperature
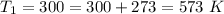
The value of k is
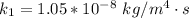
at temperature
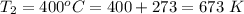
The value of k is
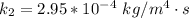
The rate constant is mathematically represented as
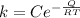
Where Q is the activation energy
R is the ideal gas constant with a value of
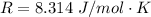
C is a constant
T is the temperature
For the first rate constant
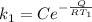
For the second rate constant
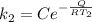
Now the ratio between the two given rate constant is
![(k_1 )/(k_2) = e^{((Q)/(R) [(1)/((T_2 - 1)/(T_1) ) ] )}](https://img.qammunity.org/2021/formulas/physics/high-school/yszu303lisvl4ekkuk3j13upnzuj80fc0v.png)
=>
![ln [(k_1)/(k_2) ] = (Q)/(R) * [(1)/((T_2 -1)/(T_1) ) ]](https://img.qammunity.org/2021/formulas/physics/high-school/pqnp04gx5sdnqiyy4hagi1af4noyq9b2rb.png)
substituting values
![ln [(1.05 *10^(-8))/(2.95 *10^(-4)) ] = (Q)/(8.314) * [(1)/((673 -1)/(573) ) ]](https://img.qammunity.org/2021/formulas/physics/high-school/ar6nb8v9xb5go9esln5v18a273tmwzvaxp.png)
=>