Question

Paul deposited $7,976 into a bank account that earns 2 5/8% compound interest annually. Calculate Paul’s interest and total after 42 months.

Answer 1

Paul’s interest and total after 42 months is $757.16 and $8,733.16 respectively.

Explanation:

We are given that Paul deposited $7,976 into a bank account that earns
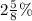`2(5)/(8)\%` compound interest annually.

Let P = Principal sum of money

R = Rate of interest p.a.

T = Time period

A = Amount of money

C.I. = Compound Interest

As, we know that amount formula for compound interest is given by;

`\text{Amount}=\text{Principal}* (1+ \text{Rate of interest})^{\text{Time}}`

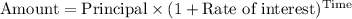
Or

`\text{A}=\text{P}* (1+ \text{R})^{\text{T}}`

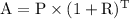
Now, in the question we are given P = $7,976 , R =
`2(5)/(8)\%` =
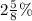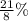`(21)/(8) \%` and T = 42 months.

So,
`\text{A}=\text{P}* (1+ \text{R})^{\text{T}}`

`\text{A}=7,976* (1+ (21)/(8 * 100) )^{(42)/(12) }`

`\text{A}=7,976* ( (821)/(800) )^{(42)/(12) }`

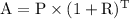
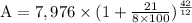
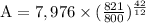
A = $8733.16

Hence, the total amount of money after 42 months is $8733.16.

Now, Compound Interest is calculated as;

`\text{Amount}=\text{Principal}+ \text{Compound interest}`

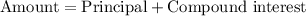
$8,733.16 = $7,976 + C.I.

C.I. = $8,733.16 - $7,976 = $757.16

Therefore, Paul’s interest and total after 42 months is $757.16 and $8,733.16 respectively.