Question

Which statement is true about the extreme value of the given quadratic equation? A. The equation has a maximum value with a y-coordinate of -21. B. The equation has a maximum value with a y-coordinate of -27. C. The equation has a minimum value with a y-coordinate of -21. D. The equation has a minimum value with a y-coordinate of -27.

Answer 1

A. The equation has a maximum value with a y-coordinate of -21.

Explanation:

From the given equation:

`\mathbf{y = -3x^2 + 12x -33}`

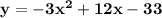
This parabola is vertical and is goes downward via the negative path

Where the vertex represents the maximum value;

`\mathbf{y = -3 (x^2 + 4x) -33}`

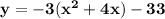
Using completing the square method;

`\mathbf{y = -3 (x^2 + 4x+2^2) -33+12}`

`\mathbf{y = -3 (x^2 + 4x+4) -21}`

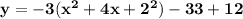
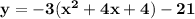
To perfect square:

`\mathbf{y = -3 (x-2)^2 -21}`

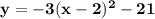
The vertex point is (2, -21)

Hence ; the equation has a maximum value with a y-coordinate of -21.