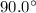Question

URGENT!!

Find the measure of angle C, to the nearest tenth of a degree, on a triangle with side lengths of a=5, b=12, c=13

A. 78.0°
B. 87.3°
C. 90.0°
D. 115.2°

Answer 1

Correct answer is option C.
`90.0^\circ`

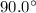
Explanation:

We are given a
`\triangle ABC` and

the side lengths as following:

`a=5,\\b=12, \\c=13`

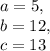
We have to find the
`\angle C` i.e. the angle which is opposite to side c.

Formula for cosine rule:

`cos C = (a^(2)+b^(2)-c^(2))/(2ab)`

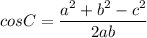
Where

a is the side opposite to
`\angle A`

b is the side opposite to
`\angle B`

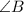
c is the side opposite to
`\angle C`

`\Rightarrow cos C = (5^(2)+12^(2)-13^(2))/(2 * 5 * 12)\\\Rightarrow cos C = (25+ 144 -169)/(120) \\\Rightarrow cos C = (169 -169)/(120) \\\Rightarrow cos C = 0\\\Rightarrow C = 90^\circ`

Please refer to the attached image for labeling and better understanding of the question.

Hence, it is a right angled triangle with
`\angle C = 90^\circ`.

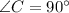Correct answer is option C.
`90.0^\circ`