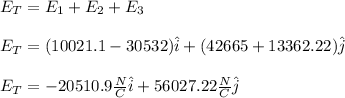Question

1.90 10-9 C charge has coordinates x = 0, y = −2.00; a 3.06 10-9 C charge has coordinates x = 3.00, y = 0; and a -4.65 10-9 C charge has coordinates x = 3.00, y = 4.00, where all distances are in cm. Determine magnitude and direction for the electric field at the origin and the instantaneous acceleration of a proton placed at the origin. (a) Determine the magnitude and direction for the electric field at the origin (measure the angle counterclockwise from the positive x-axi

Answer 1

`E_T=-20510.9(N)/(C)\hat{i}+56027.22(N)/(C)\hat{j}`

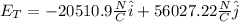
Step-by-step explanation:

The magnitude of the electric field generate by one charge is given by:

`E=k(q)/(r_2)`

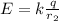
K: Coulomb's constant = 8.98*10^9 Nm^2/C^2

q: charge

r: distance to the charge that produces the electric field

You calculate the field generated by each charge at origin. Furthermore you take into account the direction of such an electric field:

charge 1 at (0,-2):

`E_1=(8.98*10^9Nm^2/C^2)(1.90*10^(-9)C)/((0.02)^2)\hat{j}=42665(N)/(C)\hat{j}`

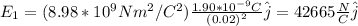
charge 2 at (3,0):

`E_2=-(8.98*10^9Nm^2/C^2)(3.06*10^(-9)C)/((0.03)^2)\hat{i}=-30532(N)/(C)\hat{i}`

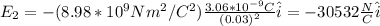
charge 3 at (3,4):

Here, it is necessary to know which is the angle between the x axis and the point. Furthermore it is necessary to calculate the distance r3 between the origin and the point:

`\theta=tan^(-1)((4)/(3))=53.13\°`

`r=√(3^2+4^2)=5cm=0.05m`

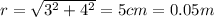
`E_3=-k(q_3)/(r_3^2)cos\theta \hat{i}+-k(q_3)/(r_3^2)sin\theta \hat{j}\\\\E_3=(8.98*10^9Nm^2/C^2)((4.65*10^(-9)C)/((0.05m)^2))[cos(53.13\°)\hat{i}+sin(53.13\°)\hat{j}]\\\\E_3=[10021.1\hat{i}+13362.22\hat{j}](N)/(C)`

Finally, you sum all E1, E2 and E3 component by component an you obtain:

`E_T=E_1+E_2+E_3\\\\E_T=(10021.1-30532)\hat{i}+(42665+13362.22)\hat{j}\\\\E_T=-20510.9(N)/(C)\hat{i}+56027.22(N)/(C)\hat{j}`