Question

1. A researcher would like to learn about the difference in proportions of students and faculty who support textbook price caps. The researcher gathers a random sample of 500 students and 500 faculty members and asks whether or not they support textbook price caps. 378 students and 256 faculty members say they support capping prices. Construct a 95% confidence interval for the difference of the population proportions. Round the confidence interval limits to three decimal places.

Answer 1

Answer: (0.186, 0.298)

Explanation:

The formula to find the confidence interval for the difference of the population proportion is given by :-

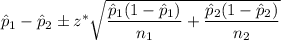`\hat{p}_1-\hat{p}_2\pm z^*\sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}` ... (i)

, where
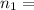`n_1=` Sample size of population 1.

`n_2=` Sample size of population 2.

`\hat{p_1}=` Sample proportion of population 1.

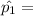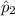`\hat{p}_2` = Sample proportion of population 2.

z* = Critical z-value corresponding to confidence interval

As per given , we have

`n_1=n_2=500`

`\hat{p}_1=(378)/(500)=0.756\\\hat{p}_2=(256)/(500)=0.512`

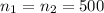
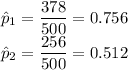
Critical value corresponds to 95% confidence interval = 1.96

Put all these values , in (i) , we get

`0.756-0.512\pm 1.96\sqrt{(0.756(1-0.756))/(500)+(0.512(1-0.512))/(500)}\\\\=0.244\pm1.96(√(0.00086864))\\\\=0.244\pm1.96(0.0294727)\\\\=0.244\pm0.0577665\\\\=(0.244-0.0577664,\ 0.24+0.0577664)\\\\=(0.1862336,\ 0.2977664)\approx(0.186,\ 0.298)`

Hence, the 95% confidence interval for the difference of the population proportions= (0.186, 0.298)