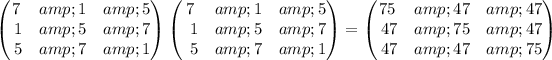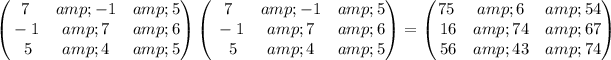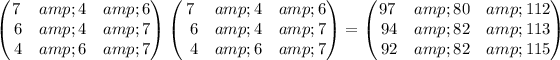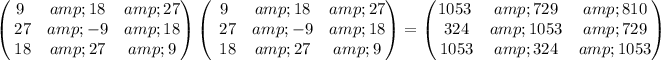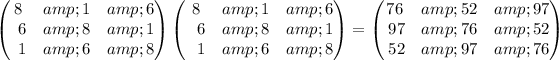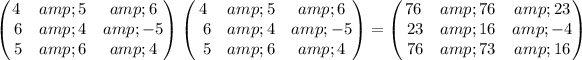Answer:
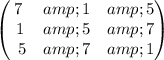 ,
,
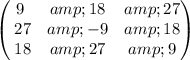 ,
,
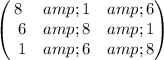 ,
,
Explanation:
Given: matrices
To find: the matrix that has identical diagonal elements
Solution:
A matrix is a rectangular array in which elements are arranged in rows and columns. Two matrices are said to be equal if their corresponding elements are equal.