Question

A company takes out an insurance policy to cover accidents that occur at its manufacturing plant. The probability that one or more accidents will occur during any given month is 0.60. The numbers of accidents that occur in different months are mutually independent. Calculate the probability that there will be at least four months in which no accidents occur before the fourth month in which at least one accident occurs.

Answer 1

0.289792.

Explanation:

If we define a month with one or more accident as "success"; and

A month with no accident as "failure" .

• P(one or more accidents will occur during any given month)=0.60.
• P(no accident will occur during any given month)=1-0.60=0.40

We want to calculate the probability that there will be at least four months in which no accidents occur before the fourth month in which at least one accident occurs.

in this case, let k=number of failures before the fourth success

Therefore,
`k\geq 4`

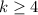
k follows a negative binomial distribution.

Therefore, the probability is:

`P(k\geq 4)=1-P(k\leq 3)\\=1-\sum_(k=0)^(3)\left(\begin{array}{ccc}3+k\\k\end{array}\right)(0.60)^4(0.40)^k\\=1-(0.60)^4 \left[\left(\begin{array}{ccc}3\\0\end{array}\right)(0.40)^0+\left(\begin{array}{ccc}4\\1\end{array}\right)(0.40)^1+\left(\begin{array}{ccc}5\\2\end{array}\right)(0.40)^2+\left(\begin{array}{ccc}6\\3\end{array}\right)(0.40)^3\right]\\=1-(0.60)^4 \left[ 1+1.6+1.6+1.28\right]\\=1-(0.60)^4[5.48]\\=0.289792`

The required probability is 0.289792.