Question

A tire company produced a batch of 6 comma 000 tires that includes exactly 220 that are defective. a. If 4 tires are randomly selected for installation on a​ car, what is the probability that they are all​ good? b. If 100 tires are randomly selected for shipment to an​ outlet, what is the probability that they are all​ good? Should this outlet plan to deal with defective tires returned by​ consumers?

Answer 1

a)
`P(X=0)`

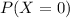
Who represent 0 defective and using the probability mass function we got:

`P(X=0) = (4C0) (0.0367)^0 (1-0.0367)^(4-0) = 0.8612`

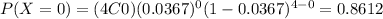
b)
`P(X=0) = (100C0) (0.0367)^0 (1-0.0367)^(100-0) = 0.02378`

For this case we can conclude that the outlet plan would deal the defectives returned by consumers

Explanation:

Let X the random variable of interest "number of defectives", on this case we now that:

`X \sim Binom(n, p)`

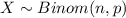
the probability of being defective for this case is given by:

`p = (220)/(6000)= 0.0367`

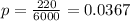
The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

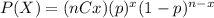
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

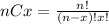
Part a

For this case n = 4 and we want to find this probability:

`P(X=0)`

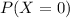
Who represent 0 defective and using the probability mass function we got:

`P(X=0) = (4C0) (0.0367)^0 (1-0.0367)^(4-0) = 0.8612`

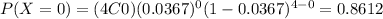
Part b

For this case n = 100 and we want to find this probability:

`P(X=0)`

Who represent 0 defective and using the probability mass function we got:

`P(X=0) = (100C0) (0.0367)^0 (1-0.0367)^(100-0) = 0.02378`

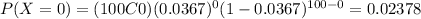
For this case we can conclude that the outlet plan would deal the defectives returned by consumers