Question

In a sample of 330 randomly selected PCC students it was found that 175 of them have a car. Assume this sample comes from a population that is normally distributed. a. Calculate the EBP then construct a 95% confidence interval estimate of the percentage of PCC students have a car (round the values of the interval to three decimal places). b. Based on your confidence interval, can we conclude that most students at PCC own a car?

Answer 1

a)
`0.530 - 1.96\sqrt{(0.530(1-0.530))/(330)}=0.47615`

`0.530 + 1.96\sqrt{(0.530(1-0.530))/(330)}=0.58385`

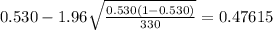
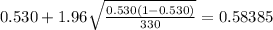
And if we convert this interval into % we got (47.615%, 58.385%)

b) For this case since the lower value for the confidence interval is a value lower than 0.5 (50%) we don't have enough evidence to conclude at 10% of significance than most students at PCC own a car

Explanation:

We can begin calculating the best estimator for the true proportion of students at PCC who own a car:

`\hat p = (175)/(330)=0.530`

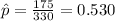
Part a

The confidence level is 95% , and the significance level would be given by
`\alpha=1-0.95=0.05` and
`\alpha/2 =0.025`. And the critical values would be given by:

`z_(\alpha/2)=-1.96, z_(1-\alpha/2)=1.96`

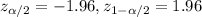
The confidence interval for the true proportion is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

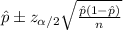
Replacing the info given we got:

`0.530 - 1.96\sqrt{(0.530(1-0.530))/(330)}=0.47615`

`0.530 + 1.96\sqrt{(0.530(1-0.530))/(330)}=0.58385`

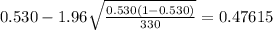
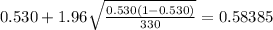
And if we convert this interval into % we got (47.615%, 58.385%)

Part b

For this case since the lower value for the confidence interval is a value lower than 0.5 (50%) we don't have enough evidence to conclude at 10% of significance than most students at PCC own a car