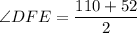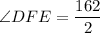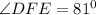Answer:
The measure of
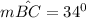
The measure of
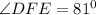
Explanation:
The correct question is added in the diagram below.
From the diagram;
Given that:
∠A = 55°
∠P =38°
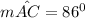
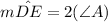
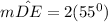
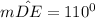
a) it is clear and obvious that ∠P is formed at the exterior of the circle; so:
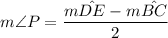
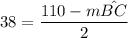
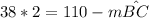
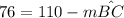
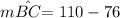
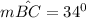
b)
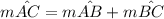
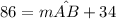
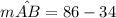
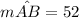
∴
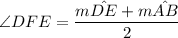 (rule: chord intersecting inside the circle)
(rule: chord intersecting inside the circle)