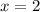Question

Can anyone help with Discriminants in math??

(“number and types of solutions” is what the rest says)

Answer 1

#1

• 3x²-3x+2

D:-

• b²-4ac
• (-3)²-4(3)(2)
• 9-24
• -15

D<0 so unequal and un real roots

#2

• b²-4ac
• (-10)²-4(1)(1)
• 100-4
• 96

D>0 so unequal and real roots

#3

• (-4)²-4(4)(1)
• 16-16
• 0

Equal and real roots

Answer 2

Discriminant

`b^2-4ac\quad\textsf{when}\:ax^2+bx+c=0`

`\textsf{when }\:b^2-4ac > 0 \implies \textsf{two real solutions}`

`\textsf{when }\:b^2-4ac=0 \implies \textsf{one real solution}`

`\textsf{when }\:b^2-4ac < 0 \implies \textsf{no real solutions}`

------------------------------------------------------------------------------------------------

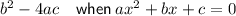
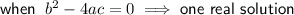
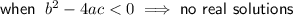
Question 5

Given function:
`f(x)=3x^2-3x+2`

`\implies a=3, \quad b=-3, \quad c=2`

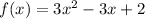
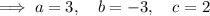
Inputting these values into the discriminant:

`\implies \textsf{discriminant}= (-3)^2-4(3)(2)=-15`

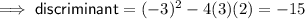
As -15 < 0 there are no real solutions

------------------------------------------------------------------------------------------------

Question 6

Given function:
`f(x)=x^2-10x+1`

`\implies a=1, \quad b=-10, \quad c=1`

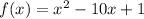
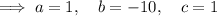
Inputting these values into the discriminant:

`\implies \textsf{discriminant}= (-10)^2-4(1)(1)=96`

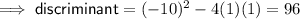
As 96 > 0 there are two real solutions

at
`x=5 \pm 2√(6)`

------------------------------------------------------------------------------------------------

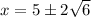
Question 7

Given function:
`f(x)=x^2-4x+4`

`\implies a=1, \quad b=-4, \quad c=4`

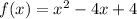
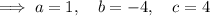
Inputting these values into the discriminant:

`\implies \textsf{discriminant}= (-4)^2-4(1)(4)=0`

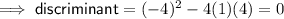
As 0 = 0 there is one real solution

at
`x=2`