Answer:
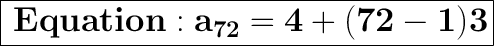

Explanation:
Let the series be: 4, 7, 10, 13,.....
Given,
- First term (a) = 4
- Common difference (d) =
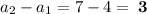
- Number of terms (n) = 72
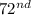 term of the series (
term of the series (
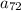 ) = ?
) = ?
We know that,
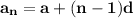
Equation for the
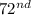 term of the series,
term of the series,
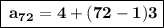
By using this formula & substituting the values,

•°• The
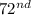 term of the series is 217.
term of the series is 217.
