Question

Suppose a sample of 100 families of four vacationing at Niagara Falls resulted in sample mean of $282.45 spent per day and a sample standard deviation of $64.50. Develop a 95% confidence interval estimate of the true population mean amount spent per day by a family of four visiting Niagara Falls. (answer in 2 decimals) SHOW YOUR WORK and write your answer in a complete sentence.

Answer 1

Given Information:

Mean = μ = $282.45

Standard deviation = σ = $64.50

Sample size = n = 100

Confidence level = 95%

Required Information:

95% Confidence interval = ?

Answer:

95% Confidence interval = ($269.81, $295.09)

Explanation:

We are given a Normal Distribution, which is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell shaped curve represents the probability.

What is Confidence Interval?

The confidence interval represents an interval that we can guarantee that the target variable will be within this interval for a given confidence level.

The confidence interval is given by

`CI = \bar{x} \pm MoE\\`

Where
`\bar{x}` is the mean and MoE is the margin of error given by

`MoE = z_(\alpha/2)((\sigma)/(√(n) ) ) \\`

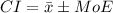
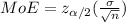
Where σ is the standard deviation, n is the sample size and
`z_(\alpha/2)` is the z-score corresponding to 95% confidence level.

`z_(\alpha/2) = 1 - 0.95 = 0.05/2 = 0.025\\\\z_(0.025) = 1.96`

`MoE = 1.96\cdot (64.50)/(√(100) ) \\\\MoE = 1.96\cdot 6.45\\\\MoE = 12.64\\`

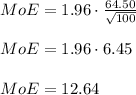
Finally, the confidence interval is

`CI = \bar{x} \pm MoE\\\\CI = 282.45 \pm 12.64\\\\CI = 282.45 - 12.64 \: and \: 282.45 + 12.64\\\\CI = \$269.81 \: and \:\:\$295.09\\`

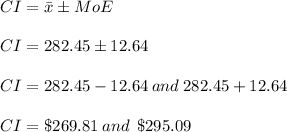
Therefore, we are 95% sure that the true population mean amount spent per day by a family of four visiting Niagara Falls is within the interval of ($269.81, $295.09)