Answer:
0.1197 = 11.97% probability that exactly 10 of the 12 individuals favor building the health center
Explanation:
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
66% of the community favored building a health center in their neighborhood.
This means that
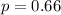
12 citizens
This means that

What is the probability that exactly 10 of the 12 individuals favor building the health center?
This is P(X = 10).


0.1197 = 11.97% probability that exactly 10 of the 12 individuals favor building the health center