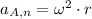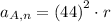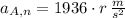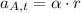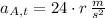Answer:
a)
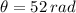 , b)
, b)
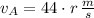 , c)
, c)
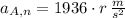 ,
,
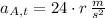
Step-by-step explanation:
a) The angular motion is obtained by integrating the angular acceleration function twice:
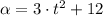
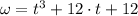
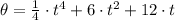
The angular motion when t = 2 s. is:
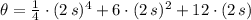
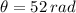
b) Let be
 the distance between A and the rotation axis, measured in meters. The magnitude of the angular velocity when t = 2 s. is:
the distance between A and the rotation axis, measured in meters. The magnitude of the angular velocity when t = 2 s. is:
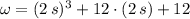
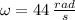
Finally, the magnitude of the velocity is:
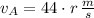
c) The angular acceleration of the disk when t = 2 s. is:
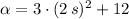
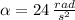
Lastly, the normal and tangential components at point A are, respectively: