Question

a textbook search committee is condisdering 10 books for possible adoption. The committee has decided to select 5 of the ten for further consideration. in how many ways can it do so

Answer 1

∴ Number of ways to select 5 books from 10 books for adoption is 252 .

Explanation:

A Permutation is an ordered Combination. When the order does matter it is a Permutation. There are basically two types of permutation:

• Repetition is Allowed: such as above. It could be "555".

• No Repetition: for example the first three people in a running race. You can't be first and second.

Formula is given by:

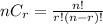`nC_r= (n!)/(r! (n-r)!)`, where n is the number of things to choose from, and we choose r of them, no repetitions, order matters. Here , n=10 , r=5.

⇒
`10C_5 = (10!)/(5!(10-5)!)`

⇒
`10C_5 = (10!)/(5!(5)!)`

⇒
`10C_5 = 252`

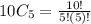
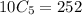
∴ Number of ways to select 5 books from 10 books for adoption is 252 .

Answer 2

They can do so in 252 ways.

Explanation:

The order in which the books are chosen is not important. So we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this question:

5 books from a set of 10. So

`C_(10,5) = (10!)/(5!(10-5)!) = 252`

They can do so in 252 ways.