Question

A club consisting of 6 juniors and 8 seniors is to be formed from a group of 13 juniors and 16 seniors. How many different clubs can be formed from the group?

Answer 1

Answer: 22,084,920 different clubs

Explanation:

The club must have 6 juniors and 8 seniors

We have a total of 13 juniors and 16 seniors.

Now, we know that the possible combinations of N objects into a group of K is equal to:

`C = (N!)/((N-K)!*K!)`

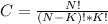
For the juniors we have N = 13 and K = 6

`Cj = (13!)/(7!*6!) = (13*12*11*10*9*8)/(6*5*4*3*2*1) = 1716`

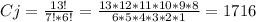
For the seniors we have N = 16 and K = 8

`Cs = (16!)/(8!8!) = (16*15*14*13*12*11*10*9)/(8*7*6*5*4*3*2*1) = 12870`

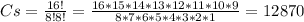
Now, as the group consist on both combinations togheter, the number of different clubs that can be formed are:

C = Cj*Cs = 1,716*12,870 = 22,084,920