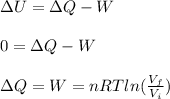Question

An ideal monatomic gas at temperature T is held in a container. If the gas is compressed isothermally, that is at constant temperature, from a volume of Vi to Vf ,

a) What is the change in the (internal) energy of the gas?
b) How much work has been done on the gas?
c) Has heat been transferred into or out of the gas during the process? If so, how much?
d) Show that the 1st law of thermodynamics is satisfied.

Answer 1

a) 0 J

b) W = nRTln(Vf/Vi)

c) ΔQ = nRTln(Vf/Vi)

d) ΔQ = W

Step-by-step explanation:

a) To find the change in the internal energy you use the 1st law of thermodynamics:

`\Delta U=\Delta Q-W`

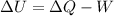
Q: heat transfer

W: work done by the gas

The gas is compressed isothermally, then, there is no change in the internal energy and you have

ΔU = 0 J

b) The work is done by the gas, not over the gas.

The work is given by the following formula:

`\\W=nRTln((V_f)/(V_i))`

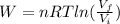
n: moles

R: ideal gas constant

T: constant temperature

Vf: final volume

Vi: initial volume

Vf < Vi, then W < 0 and the work is done on the gas

c) The gas has been compressed. Thus, its temperature increases and heat has been transferred to the gas.

The amount of heat is equal to the work done W

d)

`\Delta U = \Delta Q-W\\\\0=\Delta Q-W\\\\\Delta Q=W=nRTln((V_f)/(V_i))`