Question

A circle is cut into congruent sections and arranged to form a figure that approximates a parallelogram. Find the approximate height of the figure when its area is 12.25π square centimeters.

Answer 1

The height is 3.43 centimeters, approximately.

Explanation:

Notice that there are 16 pieces from the circle, which means each sector has an angle of

`\theta = (360\°)/(16)=22.5\°`

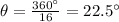
Where all sectors have equal area.

Now, the area of the whole circle is
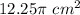`12.25 \pi \ cm^(2)`, if we use the formula of its area, we'll find the radius of the circle

`A= \pi r^(2)\\ 12.25\pi = \pi r^(2)\\ r=√(12.25) \approx 3.5`

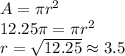
Notice that each piece works as an isosceles triangle, because each side is the radius, that is, they have the same length. So far, we know the sides of the isosceles triangle and one internal angle.

To find the height of the one piece, we need to use trigonometric reasons, because the height divides a triangle in two equal right triangles.

`cos(11.25\°)=(h)/(3.5)\\ h=3.5 * cos(11.25 \°)\\h \approx 3.43`

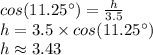
Therefore, the height is 3.43 centimeters, approximately.