Question

Central High's enrollment increases at an average rate of 100 students per year, while Washington High's enrollment increases at an average rate of 300 students per year. Central High has 3000 students and Washington High has 2000 students. If enrollments continue to change at the same rate, when will the two schools have the same number of students?

Answer 1

The two schools will have the same number of students in 5 years.

Explanation:

The number of students for both these schools, after t years, can be modeled by linear functions.

Central High:

Currently has 3000 students.

Enrollment increases at an average rate of 100 students per year.

So after t years, the number of students that Central High will have is:

`C(t) = 3000 + 100t`

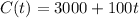
Washington High:

Currently has 2000 students.

Enrollment increases at an average rate of 300 students per year.

So after t years, the number of students that Washington High will have is:

`W(t) = 2000 + 300t`

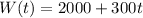
If enrollments continue to change at the same rate, when will the two schools have the same number of students?

We have to find t for which:

`C(t) = W(t)`

So

`3000 + 100t = 2000 + 300t`

`200t = 1000`

`t = (1000)/(200)`

`t = 5`

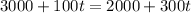
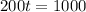
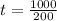
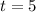
The two schools will have the same number of students in 5 years.