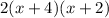Answer:
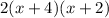
Explanation:
We can start with the observation that every coefficent in the quadratic
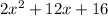 is a multiple of 2. Factoring out the 2, our expression becomes
is a multiple of 2. Factoring out the 2, our expression becomes
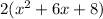 . Let's focus on the second term,
. Let's focus on the second term,
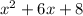 . To factor this, we want to find two numbers that multiply to 8 and add to 6. 4 · 2 = 8 and 4 + 2 = 6, so we can use that fact to split the middle term and factor the quadratic completely:
. To factor this, we want to find two numbers that multiply to 8 and add to 6. 4 · 2 = 8 and 4 + 2 = 6, so we can use that fact to split the middle term and factor the quadratic completely:
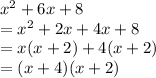
Putting that back with the 2 we factored out earlier, our fully factored function is