Answer:
The area of the full figure is 60 square inches.
Explanation:
There are 4 triangles and one square in this figure. We can start by figuring out the area of the middle square, which would be
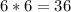 because we know the sides are all 6 inches.
because we know the sides are all 6 inches.
Next, we can look at the triangles and see that their hypotenuses (the longest sides) are all the same length, that being 5 inches. This means that we only need to find the length of the third side and then multiply the area of one triangle by 4 to get the area of all the triangles.
The pythagorean theorem states that in any right triangle,
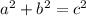 , with
, with
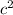 being the length of the hypotenuse. Since we know the length of the hypotenuse is 5 and one of the legs of the triangle is 4, we can insert this into the equation:
being the length of the hypotenuse. Since we know the length of the hypotenuse is 5 and one of the legs of the triangle is 4, we can insert this into the equation:
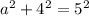 , which when simplified all the way gives us that
, which when simplified all the way gives us that
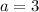 .
.
Since a right triangle is half of a rectangle, the easiest way to find the area of the triangle is to multiply the measures of the two legs together and then divide by two:
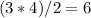 . Therefore, we know that each triangle in the picture has an area of 6.
. Therefore, we know that each triangle in the picture has an area of 6.
Finally, you need to add all of the areas together to find the area of the full figure:
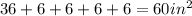
The area of the full figure is 60 square inches.
Hope this helps! :)