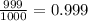Answer:
The probability of not winning the game is
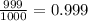
Explanation:
The probability of winning a game =
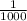
We are supposed to find the probability of not winning the game
Property : Sum of all probabilities is 1
So, let the probability of not winning the game be x
So,
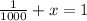
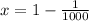
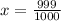
So,the probability of not winning the game =
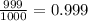
Hence the probability of not winning the game is