Answer:
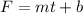
From the info given we know that m =-11 and we have a condition given:
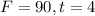
Using this condition we have:
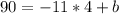
And solving for b we got:
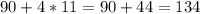
So then the original temperatue for this case is 134 F
Explanation:
For this case we know that after four hours the temperature was 90 f and the temperature dropped 11 f per hour.
We can use a linear model to solve the problem given by:
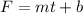
Where F represent the temperature, t the time in hours and m the slope and b the intercept.
From the info given we know that m =-11 and we have a condition given:
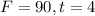
Using this condition we have:
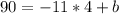
And solving for b we got:
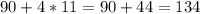
So then the original temperatue for this case is 134 F