Question

Determine the amplitude, period, and phase shift of the function f(x)=cos (8(x-1))+2​

Answer 1

We have been given a function
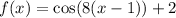`f(x)=\text{cos}(8(x-1))+2`. We are asked to find the amplitude, period and phase shift of the function

We can see that our given function is in form
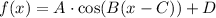`f(x)=A\cdot \cos(B(x-C))+D`, where,

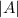`|A|` = Amplitude.

Period =
`(2\pi)/(|B|)`

C = Horizontal shift,

D = Vertical shift.

We can see that value of a is 1, therefore, the amplitude of given function would be 1.

We can see that B is equal to 8, so we will get:

`\text{Period}=(2\pi)/(|B|)= (2\pi)/(|8|)=(\pi)/(4)`

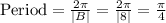
Therefore, the period of given function is
`(\pi)/(4)`.

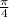Since the value of C is 1, therefore, horizontal shift is 1.

Since the value of D is 2, therefore, vertical shift would be 2.