Question

Se tiene un lote baldío de forma triangular bardeado. La barda de enfrente tiene una medida de 4 m,las otras dos bardas no es posible medirlas directamente pues hay mucha basura. Sin embargo,se sabe que el ángulo que está frente a la barda frontal mide 34° y otro de sus ángulos mide 64°. Se quiere calcular la medida de la barda que está enfrente del ángulo de 64°. Explica por qué no es posible resolver el problema aplicando sólo las razones trigonométricas o el teorema de Pitágoras

Answer 1

a) La medida de la barda que está enfrente del ángulo 64° es de, aproximadamente, 6.4292m. b) El triángulo en cuestión no es un triángulo rectángulo, es decir, ninguno de sus ángulos internos es recto (90 grados sexagesimales). En estos casos, no se puede aplicar el Teorema de Pitágoras o la simple utilización de las razones trigonométricas; se aplican, en cambio, leyes para la resolución de triángulos oblicuángulos (o triángulos no rectángulos).

Explanation:

Este problema no se puede resolver "aplicando sólo las razones trigonométricas o el teorema de Pitágoras" porque es sólo aplicable a triángulos rectos, es decir, uno de los ángulos del triángulo es recto o igual a 90 grados sexagesimales. Los dos restantes triángulos suman 90 grados sexagesimales, o se dice, son complementarios.

La resolución de triángulos que no son rectos (conocida en algunos textos como solución de problemas de triángulos oblicuángulos) pueden resolverse usando, la ley de los senos (o teorema del seno), ley de los cosenos y la ley de las tangentes. El caso propuesto en la pregunta se ajusta a la ley de los senos:

`\\ (a)/(\sin(\alpha)) = (b)/(\sin(\beta)) = (c)/(\sin(\gamma))`

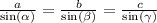
Es decir, la razón entre el lado de un triángulo y el seno del ángulo que tiene frente a él es igual para todos los lados y ángulos del triángulo.

El triángulo de la pregunta no tiene un ángulo recto

La suma de los ángulos internos de un triángulo es de 180 grados sexagesimales:

`\\ \alpha + \beta + \gamma = 180^(\circ)`

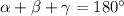
En la pregunta tenemos que la suma de los dos ángulos propuestos es:

`\\ 34^(\circ) + 64^(\circ) + \gamma = 180^(\circ)`

`\\ 98^(\circ) + \gamma = 180^(\circ)`

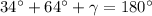
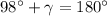
Restando 98 grados sexagesimales a cada lado de la igualdad:

`\\ 98^(\circ) - 98^(\circ) + \gamma = 180^(\circ) - 98^(\circ)`

`\\ 0 + \gamma = 180^(\circ) - 98^(\circ)`

`\\ \gamma = 82^(\circ)`

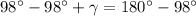
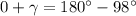
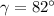
Con lo que se deduce que no hay ningún ángulo recto en el triángulo propuesto y no se podría usar el Teorema de Pitágoras o simples razones trigonométricas para resolverlo.

Resolución del lado del triángulo

De la pregunta tenemos:

• La barda de enfrente tiene una medida de 4m. El ángulo que está enfrente de esta barda (barda frontal) es de 34°.
• No se sabe el valor del lado que está enfrente del ángulo de 64°, pero se puede calcular usando la Ley de los senos.

Digamos que:

`\\ a = 4m, \alpha = 34^(\circ)`

`\\ b = x, \beta = 64^(\circ)`

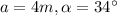
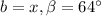
Entonces, aplicando la Ley de los senos:

`\\ (a)/(\sin(\alpha)) = (b)/(\sin(\beta))`

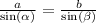
Multiplicando a cada lado de la igualdad por
`\\ \sin(\beta)`

`\\ (a)/(\sin(\alpha))*\sin(\beta) = (b)/(\sin(\beta))*\sin(\beta)`

`\\ (a)/(\sin(\alpha))*\sin(\beta) = b*(\sin(\beta))/(\sin(\beta))`

`\\ (a)/(\sin(\alpha))*\sin(\beta) = b*1`

`\\ (a)/(\sin(\alpha))*\sin(\beta) = b`

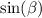
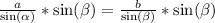
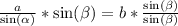
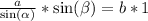
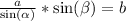
Sustituyendo cada valor en la expresión anterior:

`\\ b = (a)/(\sin(\alpha))*\sin(\beta)`

`\\ b = (4m)/(\sin(34^(\circ)))*\sin(64^(\circ))`

`\\ b = 4m*(0.8988)/(0.5592)`

`\\ b = 6.4292m`

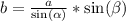
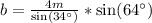
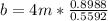
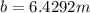
En palabras, la medida de la barda que está enfrente del ángulo 64° es de, aproximadamente, 6.4292m.

El lado c puede obtenerse de manera similar considerando que
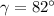`\\ \gamma = 82^(\circ)`.