Question

A circle has a sector with area 33 pi and a central angle of 11/6 pi radians. What is the area of a circle?

Answer 1

`A_(circle)= (2\pi *33 \pi)/((11 \pi)/(6))= 36\pi`

Then we can conclude that the area for the circle would be
`36\pi`

Explanation:

For this case we know that a sector have an area of
`33\pi` with a central angle of
`x=(11\pi)/(6)`

We know that the total area of a cricle is
`A= \pi r^2` and we want to find the area of the circle and we can use the following proportional rule:

`A_s = (x)/(2\pi) A_(circle)`

From the last equation we can solve for
`A_(circle)` and we got:

`A_(circle)= (2\pi A_s)/(x)`

And replacing we got:

`A_(circle)= (2\pi *33 \pi)/((11 \pi)/(6))= 36\pi`

Then we can conclude that the area for the circle would be
`36\pi`

Answer 2

36π

Explanation:

The area of a circle is given as:

`A = \pi r^2`

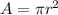
where r = radius of the circle

The area of a sector of a circle is given as:

`A_s = (\alpha )/(2\pi) * \pi r^2`

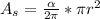
where α = central angle in radians

Since
`\pi r^2` is the area of a circle, A, this implies that:

`A_s = (\alpha )/(360) * A`

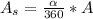
A circle has a sector with area 33 pi and a central angle of 11/6 pi radians.

Therefore, the area of the circle, A, is:

`33 \pi = ((11 \pi)/(6) )/(2 \pi) * A\\\\33\pi = (11)/(12) * A\\\\=> A = (33\pi * 12)/(11)\\ \\A = (396 \pi)/(11) \\\\A = 36\pi`

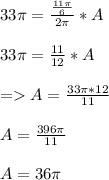
The area of the circle is 36π.