Question

The equation y - 7/2 = 1/2(x-4) is written in point-slope form. What is the y-intercept of the equation?

Ο -11/2

Ο -1/2

Ο 1/2

Ο 3/2

Answer 1

`y - (7)/(2)= (1)/(2) (x-4)`

`y-(7)/(2)= (1)/(2)x - 2`

`y = (1)/(2)x -2 + (7)/(2)`

`y = (1)/(2)x + (3)/(2)`

`y = mx +b`

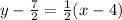
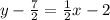
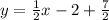
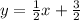
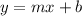
Is given by:

Ο 3/2

Explanation:

For this case we have the following function given:

`y - (7)/(2)= (1)/(2) (x-4)`

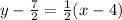
If we distribute the 1/2 in the right we got:

`y-(7)/(2)= (1)/(2)x - 2`

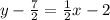
Now we can add on both sides 7/2 and we got:

`y = (1)/(2)x -2 + (7)/(2)`

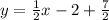
And simplifying we got:

`y = (1)/(2)x + (3)/(2)`

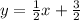
And the answer for this case using the general formula:

`y = mx +b`

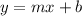
Is given by:

Ο 3/2