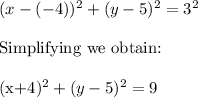Question

You have a tree in your yard 4 ft to the left of and 5 ft in front of the corner of your porch. A circular fence 3 ft in radius has its center at the tree. If the corner of your porch is the origin and forward is the positive y direction, what equation represents the circle formed by the fence in your yard?

Answer 1

`(x+4)^2+(y-5)^2=9`

Explanation:

If the corner of your porch is the origin

• 4 ft to the left, x=-4
• 5 ft in front, y=5

The tree's location is at (-4,5).

• A circular fence 3 ft in radius has its center at the tree(-4,5).

We want to determine the equation of a circle with center (-4,5) and radius 3 ft.

The equation of a circle center (h,k) with a radius of r is given as:

`(x-h)^2+(y-k)^2=r^2`

(h,k)=(-4,5), r=3

The equation formed by the fence therefore is:

`(x-(-4))^2+(y-5)^2=3^2\\\\$Simplifying we obtain:\\\\(x+4)^2+(y-5)^2=9`