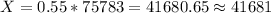Answer:
a)
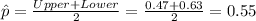
b)
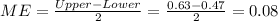
c) For this case in order to find the number of people who would support the bike lanes we just need to multiply the estimated proportion by the total size and we got:
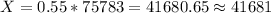
Explanation:
For this case we have an interval for the true proportion of adults in a certain town who want to add bike lanes to a major roadway:
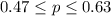
Part a
For this case the point of estimate is given by:
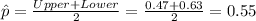
Part b
We can estimate the margin of error with this formula:
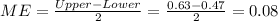
Part c
For this case in order to find the number of people who would support the bike lanes we just need to multiply the estimated proportion by the total size and we got: